RAPID:NSF-BSF: Analysis of the spreading patterns and the efficiency of quarantine measures for COVID-19, based on available world-wide spatio-temporal data

This project is supported by NSF, through the Ecology and Evolution of Infectious Diseases Program in the Division of Environmental Biology, using funds from the Coronavirus Aid, Relief, and Economic Security (CARES) Act, grant DEB-2035297. This project is also part of an international collaboration with Bar-Ilan University, funded through BSF. Any opinions, findings and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.

People

• Lazaros K. Gallos (PI; DIMACS, Rutgers University)
• Shlomo Havlin (PI in the BSF project; Physics, Bar-Ilan University)
• Troy McMahon (Postdoc; DIMACS, Rutgers University)
• Adrian Chan (Postdoc; Physics, Bar-Ilan University)
• Nikki Cheng (REU Student; Mt Holyoke College)

Project website

http://dimacs.rutgers.edu/~lgallos/COVID/

Description

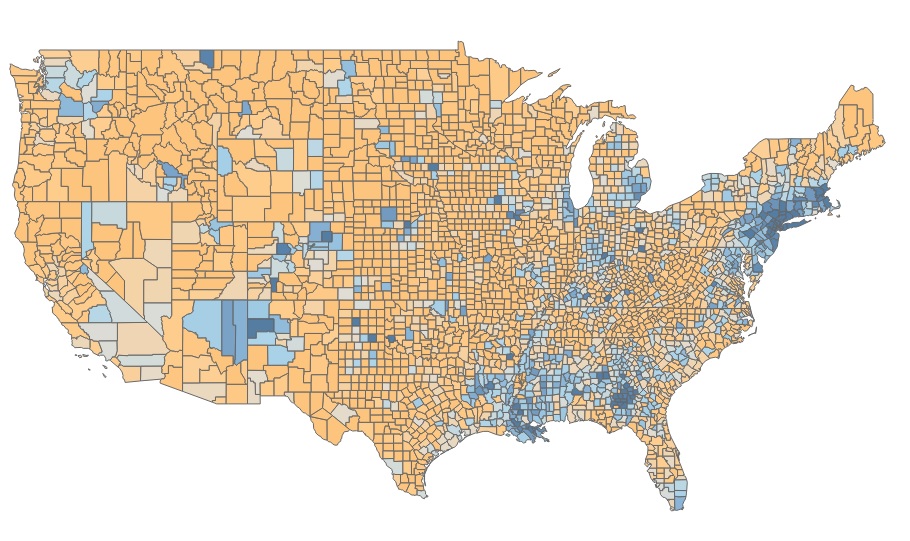
The recent COVID-19 pandemic has created an urgent need to understand the spread of coronavirus (SARS-CoV-2). The special features of this virus and the unprecedented global response present potentially novel paths of disease transmission that have not been observed in modern times. These paths create continuously evolving spatial and temporal patterns of observable properties, such as number of infections or virus-related deaths. Using tools from statistical physics and network science, this project seeks to understand the special features of this complex behavior and to compare these patterns in different geographical areas. The availability of high-resolution data will enable the construction of computational models which will attempt to explain these patterns in terms of quarantine measures, timing of such measures, and environmental conditions. Such an understanding could assess the efficiency of quarantine measures implemented around the world and also identify the effects of temperature and humidity. This project aims to make these mathematical and computational tools be readily available at a next possible outbreak wave and to allow immediate analysis of epidemiological data. The outcome of this research has the potential of providing early detection of geographical areas in high risk, informing thus the decisions of policy makers. This project also provides significant opportunities for the training of STEM researchers.
The research will focus on the scaling and correlation behavior of epidemic characteristics between different areas. The scaling analysis will study how the observed quantities change for different scales of time and space, characterized by power-law exponents. Different exponents indicate different propagation patterns which can provide information about the effectiveness of location and timing of tests and enforcement of quarantine measures. Similarly, the extent of spatial correlations and their time evolution are key indicators of spreading patterns. The analysis of the correlation lengths and correlation times can indicate how close the virus spreading process is to criticality. This is particularly important because critical systems are in general much more vulnerable to rapid spreading. The data analysis will be complemented by appropriate mathematical and simulation epidemic models to test the influence of population and environmental factors on the empirical data.