October 2016
IAS/DIMACS postdoctoral fellow Noga Ron-Zewi and her collaborators Swastik Kopparty and Shubhangi Saraf, both faculty members in Computer Science and Mathematics at Rutgers,
graduate students Sivakanth Gopi and Rafael Oliveira of Princeton University, and Or Meir of the University of Haifa have made several recent breakthroughs in the study of local codes.
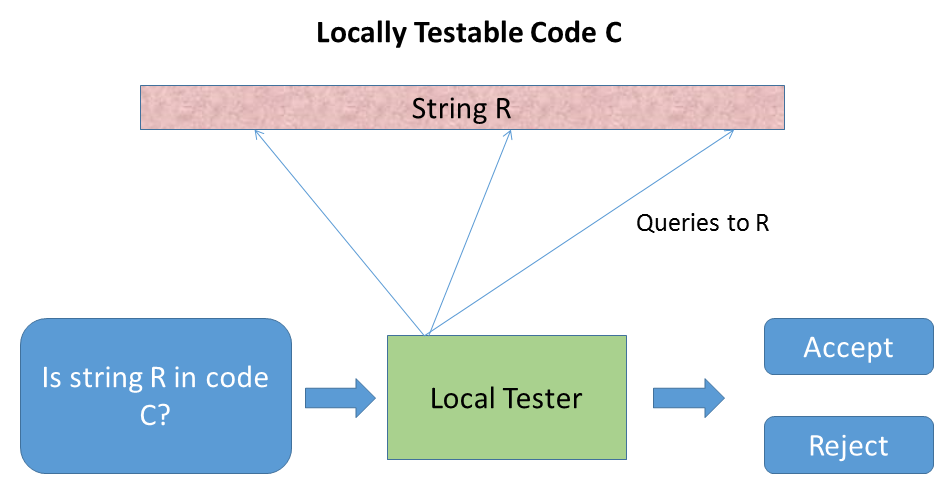
In today’s world, huge amounts of data need to be reliably stored or transmitted, but a certain amount of noise or corruption is inevitable. An error-correcting code is a scheme for robustly representing data in the form of codewords that allows one to detect and correct errors in transmission. Locally testable and locally decodable codes are special families of error-correcting codes that admit highly efficient algorithms for error detection and correction. In contrast to classical error-correcting codes that must examine an entire transmission in order to detect or correct errors, these codes enable detecting and correcting errors with high probability in sublinear time by probing only a small number of entries of a corrupted codeword.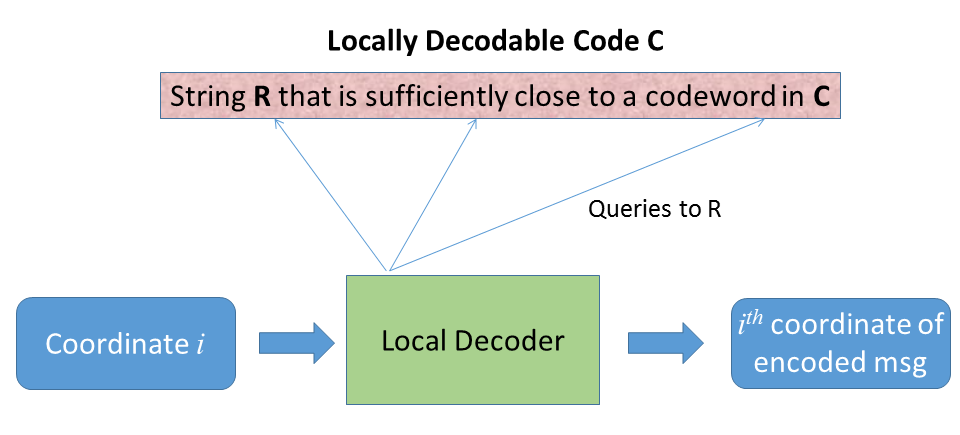 
Locally testable and locally decodable codes have been intensely studied for the past two decades with numerous applications to complexity theory, but their relevance to transmission and storage of massive data and the use of local codes in cloud storage systems has heightened recent interest.
Locally decodable codes provide a method to encode k-bit messages into n-bit codewords such that even after a constant fraction of the bits of the codeword get corrupted, any bit of the original message can be recovered by looking at a small number of bits of the corrupted codeword. Similarly, locally testable codes provide a method to encode k-bit messages into n-bit codewords such that there is an efficient tester that can query an n-bit string in only a small number of bits and decide whether the string is near or far from a true codeword. The number of queries required by such algorithms is called the query complexity and is a measure of running time. The rate of the code is defined as the ratio between k and n and measures the proportion of non-redundant information it contains.
In a paper presented at the 2016 Annual Symposium on the Theory of Computing (STOC 2016), Kopparty, Meir, Ron-Zewi and Saraf substantially improved the query complexity of such codes. Specifically, their work provides an exponential improvement on the best-known query complexity of locally testable and locally decodable codes. It describes new families of locally testable codes of constant rate that can detect a constant fraction of errors with query complexity (log n)O(loglog n) for a transmission of length n, and new families of locally decodable codes of constant rate that can correct a constant fraction of errors with query complexity exp(√log n). Prior to their work, the best known query complexity for such codes was of the form nc for a constant c > 0 that can be arbitrarily close to 0.
Ron-Zewi and her collaborators also showed that their codes can achieve stronger trade-offs between rate and error correction capability than were known previously. Over large alphabets (of constant size), their codes approach the Singleton bound, meaning that they achieve a tradeoff between rate and error correction capability that is essentially best-possible for general error-correcting codes. In follow-up work to be presented at the 28th Annual ACM-SIAM Symposium on Discrete Algorithms (SODA 2017), Gopi, Kopparty, Oliviera, Ron-Zewi, and Saraf showed that such codes can also approach the Gilbert-Varshamov bound which is the best known trade-off over the binary alphabet. This has the surprising consequence that asking for a large-alphabet error-correcting code to also be locally decodable or locally testable does not require any sacrifice in terms of rate and error correction capability.
As an IAS/DIMACS postdoctoral fellow, Ron-Zewi spent the 2014-15 academic year at the Institute for Advanced Study (IAS) and the 2015-16 academic year at DIMACS. In a brief update for the IAS Newsletter, Avi Wigderson described the results saying, “For both testing and decoding, new codes were designed with rate approaching 1 (namely, negligible redundancy), for which the number of queries needed is sub-polynomial! All previous constructions with such query complexity have extremely poor rate, whereas constant rate codes could only work with polynomially many queries in the blocklength.”
In 2016, Ron-Zewi joined the faculty of the computer science department at Ben-Gurion University in Israel following the completion of her postdoc at DIMACS.
The results in their STOC 2016 paper were also presented by Saraf at the DIMACS Workshop on Cryptography and its Interactions: Learning Theory, Coding Theory, and Data Structures in July and by Kopparty in a TCS+ seminar in September. A video of Kopparty’s TCS+ talk is available here. A full version of this paper is available in two parts on the ECCC: [TR15-068] [TR15-110]
The results that are to appear in their SODA 2017 paper were presented by Kopparty at the Computational Complexity workshop held at the Banff International Research Station (BIRS) in September, 2016. A video of Kopparty’s BIRS talk is here. A full version of this paper is also available on the ECCC: [TR16-122].
Printable version of this story: [PDF]
References:
S. Kopparty, O. Meir, N. Ron-Zewi, and S. Saraf, “High rate locally-correctable and locally-testable codes with sub-polynomial query complexity,” Proceedings of the 48th Annual Symposium on Theory of Computing (STOC), pages 25-32, 2016.
S. Gopi, S. Kopparty, R. Oliveira N. Ron-Zewi, and S. Saraf, “Locally testable and locally correctable codes approaching the Gilbert-Varshamov bound,” to appear in the Proceedings of the ACM-SIAM Symposium on Discrete Algorithms, 2017.